A bipartite graph is a special kind of graph that consists of two vertex sets.
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:
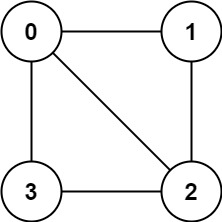
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
class BipartiteChecker:
def Bipartite(self, graph) -> bool:
glen = len(graph)
s = []
vis = [0] * glen
for i in range(glen):
if vis[i]: continue
vis[i] = 1
s.append(i)
while len(s):
curr = s.pop()
edges = graph[curr]
for next in edges:
if not vis[next]:
vis[next] = vis[curr] ^ 3
s.append(next)
elif vis[curr] == vis[next]:
return False
return True
# Driver
G = BipartiteChecker()
'''
Matrx = [[1,2,3],[0,2],[0,1,3],[0,2]]
'''
Matrx=[]
while True:
arr=list(map(str,input().split(" ")))
if arr != ['']:
Matrx.append(list(map(int,arr)))
else:
break
print("True") if G.Bipartite(Matrx) else print("False")
INPUT_1:
1 2 3
0 2
0 1 3
0 2
OUTPUT:
False
INPUT_2:
1 3
0 2
1 3
0 2
OUTPUT:
True
ILLUSTRATION

Morae Q!
- Find the number of strings made by using each alphabet as starting character.
- Find the Pythagorean triplet.
- Find out what is the minimum possible energy he needs to spend.
- Sort the array in non-decreasing order and print out the original indices of sorted array.
- Compute the number of landmasses on the planet after all the meteorites have fallen.
- Give the appropriate server status as output.
- Regular expressions (Regex) using search module in python.
- Find the minimum distance between any pair of equal elements in the array.
- Find the total number of matching pairs of socks that are available.
- Find the total number of teams which can work together and cannot work together.
- Given the heights of all the boys and girls tell whether it is possible for all boys to get a girl.
- Find the sequence of cities to visit according to coordinates and conditions.
- Find the number of unique patches of rectangular land to grow samba(rice) in.
- Regular expression Regex matching strings.
- Generate a greeting quote for admin.
- Find all the cavities on the map and replace their depths with the character X.
- Check whether the given graph is Bipartite or not.
- Find the status of the passengers and safari cars at zoo after k units of time.
- Determine the chair number occupied by the child who will receive that chocolate.
- Check if Rubik’s cube of any dimensions can be assembled.